How does the new CS2 Tradeup Algorithm work?
In Valve’s recent update on the 23rd of october for Counter-strike 2, they quietly changed the Trade Up formula regarding the odds and float calculation of the output skins. This update didn’t just change to math: it destroyed the usefullness of filler skins and fundamentally changed the way how output floats are calculated.
Table of Contents
The Changes To The Float Calculation Algorithm
The Old CS2 Trade Up Algorithm:
before the patch, the float of you output skin was calculated as a simple weighted average of the input floats:
\[
\text{Average Input Float} = \frac{\sum_{i=1}^{n} F_i}{n}
\]
Now you can input this into the following formula:
\[
\text{Output Float} = (\text{max. Float}_o – \text{min. Float}_o) \times \text{Average Input Float} + \text{min. Float}_o
\]
\[F_i = \text{float value of input skin } i\]
\[n = \text{total number of input skins}\]
The max. FLoat and min. Float reffer to the float range of the output skin so that can be 0 to 1.00 or for example 0 to 0.80. also known as “the float cap”.
Example (Old Algorithm)
10x input skins with a float of 0.30 –> Average float = (10x 0.30) / 10 = 0.30
Output skin float = 0.30 (And then you would adjust for the Float cap like shown in the formula above).
This shows that input float caps don’t have a impact on the float for the output skins.
This meant that if you use a filler skin like for example the populair filler skin: P2000 Amber Fade with a narrow float cap of (0.00 to 0.40) it wouldnt hurt the final average float.
This meant that if you use a filler skin like for example the populair filler skin: P2000 Amber Fade with a narrow float cap of (0.00 to 0.40) it wouldnt hurt the final average float. So 10x P2000 amberfade with a 0.30 float would result in a average input float of 0.30.
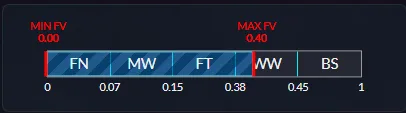
The New CS2 Trade Up Algorithm
The new Trade up Algorothm that Valve introduced is far more compex. It now accounts for the float cap of the input skins aswell when calculating the average input float of the tradeup.
Each input float is first noramalized according to its float cap before averaging the floats like before the update so the new formula is:
\[
\text{Adjusted Float}_i = \frac{F_i – F_{\text{min},i}}{F_{\text{max},i} – F_{\text{min},i}}
\]
Then, Valve calculates the average of all the adjusted floats and uses the output float range like before.
\[
\text{Output Float} = F_{\text{min,out}} +
\left(
\frac{1}{n}
\sum_{i=1}^{n}
\text{Adjusted Float}_i
\right)
\times
\left(
F_{\text{max,out}} – F_{\text{min,out}}
\right)
\]
That results in the complete formula for the new algorithm:
\[
f_{\text{out}} = F_{\text{min,out}} +
\left(
\frac{1}{n}
\sum_{i=1}^{n}
\frac{F_i – F_{\text{min},i}}{F_{\text{max},i} – F_{\text{min},i}}
\right)
\times
\left(
F_{\text{max,out}} – F_{\text{min,out}}
\right)
\]
Where:
\[F_i = \text{float value of input skin } i\]
\[n = \text{total number of input skins}\]
\[
F_{\text{min},i} = \text{minimum possible float of input skin } i
\]
\[
F_{\text{max},i} = \text{maximum possible float of input skin } i
\]
\[
F_{\text{min,out}} = \text{minimum float of the output skin}
\]
\[
F_{\text{max,out}} = \text{maximum float of the output skin}
\]
This new formula makes it so that inputskins with a restricted float like (0-0.5) are weighted differently than skins with a full float range (0-1). This makes it so that a lot of the tradeups that previously used floats caps in their advantage now are not profitbale anymore because of the adjusted input float.
Because most tradeups will have a higher average adjusted input float than before.
Example (New Algorithm)
10x input skins (P2000 amberfade) with a float of 0.30
The float cap is (0-0.40) like you can see in the image this will be relevant in the calulation.

First Normalize the float:
This shows that input float caps don’t have a impact on the float for the output skins.
\[F_i = \text{0.30} \]
\[n = \text{10}\]
\[F_{\text{min},i} = \text{0} \]
\[F_{\text{max},i} = \text{0.40} \]
\[
\text{Adjusted Float}_i = \frac{F_i – F_{\text{min},i}}{F_{\text{max},i} – F_{\text{min},i}} = \frac{0.30 – 0}{0.40 – 0} = 0.75
\]
Now we can calculate the new adjusted average float like (0.75*10)/10 = 0.75 average input float
This shows that the input skin floatcap now has a big effect on the float used in the tradeup calulation.
In this example the normal average float was 0.30 and the new adjusted average float = 0.75 that is a 2.5 times increase!#
This means that if we get an output skin with a float cap from 0 to 1 we will get a skin with a float of 0.75 compared to the 0.30 from before the update.
Probability Changes
before the update the probability for each output was based on how many outputs existed in each collection and how many skins you used from a collection.
Now, the chance for each outcome is determined solely by the number of inputs from a collection. Before, people used fillerskins in their tradeup. This where skins with as little outputs as possible to limit the chance of getting that collection. Now, this doesnt matter anymore beacuse its solely based on the number of input skins in the contract.
The new formula
\[
P(\text{output from collection } X) = \frac{\text{number of skins from a collection}}{\text{number of inputs}}
\]
So now you can just use the cheapest input skins from for example the Restricted rarity without having to worry about effecting the odds. This is disadvantageous for trade up contracts because now you cant manipulate the chances of getting a collection you want by using the correct filler skins.
FAQ
What is a float cap?
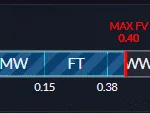
A float cap limits the range of a skin’s possible float values. For example, The P2000 amberfade can only have a float between 0 and 0.40
It cannot exist in battle scarred condition.
Why are my Trade Up results worse now?
Because the new formula now adjusts for input float ranges. Using capped inputs (like Amber Fade or Cold Blooded) increases your average float, leading to worse output conditions. Read the full article for more info.
Can I still use filler skins?
Yes, but they no longer imporve odds. This is because of the way how the probability of getting a output from a certain collection is calculated now. Its better to use the cheapest skin available of the same rarity.
What inputs should I use now instead of fillers?
Use the cheapest skins with a full 0-1 float range or better so a float range of 0.2-1 would be better and result in a lower average float.
How do I check a skin’s float range?
Websites like CSFloat or TradeUpSpy list min and max floats for every CS2 skin.
Can I still profit from Trade Ups?
Yes, but the new system makes finding profitable tradeups harder. The new update also has made a lot of tradeups non-profit that where profitable before.
What is the new formula for calculating average floats?
The new formula for calculating average floats is availiable here
What is the new formula for calculating the probability to get a certain skin form a trade up?
The new formula for calculating the probability of getting a certain about is available here
Conclusion
Valve’s recent update has fundamentally changed the way of calculating Trade Up outputs in CS2. The new float formula usese input float caps and this makes making low-float outcomes rarer and eliminates the need for tradeup fillers because of the way how the probability of getting a skin is calculated. Finding new profitable tradeups will take some time but I will make sure the upload the updated versions as fast as possible.

Hey great write up of the changes. I recently have been able to verify the change in float outcomes. However, still need to do a test which proves that the outcome chances have changed. Where did you find out that the outcome chance has changed?
Hey, I’ve seen multiple mentioning that the odds have changed, for example on https://steamcommunity.com/sharedfiles/filedetails/?id=3594575259 and https://www.youtube.com/watch?v=zqV0UfO5ofw.
I’ve also heard people (some famous youtubers dont recall which ones exactly) talk about it, and Tradeupspy.com also seems to support these findings. I saw a test somewhere for these claims but cant find the source anymore.
So my assumption is based on that data, which in my opinion looks convincing enough to be confident in posting this.
Thank you for commenting on my website, if you have any further questions or requests please do not hesitate to contact me